Rigid line inclusion
This article needs additional citations for verification. (December 2013) |
A rigid line inclusion, also called stiffener, is a mathematical model used in solid mechanics to describe a narrow hard phase, dispersed within a matrix material. This inclusion is idealised as an infinitely rigid and thin reinforcement, so that it represents a sort of ‘inverse’ crack, from which the nomenclature ‘anticrack’ derives.
From the mechanical point of view, a stiffener introduces a kinematical constraint, imposing that it may only suffer a rigid body motion along its line.
Theoretical model[edit]
The stiffener model has been used to investigate different mechanical problems in classical elasticity (load diffusion,[1] inclusion at bi material interface [2]).

The main characteristics of the theoretical solutions are basically the following.
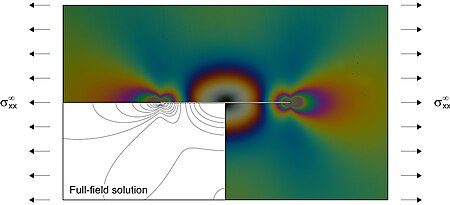
- Similarly to a fracture, a square-root singularity in the stress/strain fields is present at the tip of the inclusion.
- In a homogeneous matrix subject to uniform stress at infinity, such singularity only arises when a normal stress acts parallel or orthogonal to the inclusion line, while a stiffener parallel to a simple shear does not disturb the ambient field.
Experimental validation[edit]

The characteristics of the elastic solution have been experimentally confirmed through photoelastic transmission experiments.[3]
Interaction of rigid line inclusions[edit]
The interaction of rigid line inclusions in parallel, collinear and radial configurations have been studied using the boundary element method (BEM) and validated using photoelasticity.[4]
Shear bands emerging at the stiffener tip[edit]
Analytical solutions obtained in prestressed elasticity show the possibility of the emergence of shear bands at the tip of the stiffener.[5][6][7][8]
References[edit]
- ^ Koiter, W.T., On the diffusion of load from a stiffener into a sheet. Q. J. Mech. Appl. Math. 1955, VIII, 164–178.
- ^ Ballarini, R., A rigid line inclusion at a bimaterial interface. Eng. Fract. Mech., 1990, 37, 1–5.
- ^ Noselli, G.; Dal Corso, F.; Bigoni, D. (2010). "The stress intensity near a stiffener disclosed by photoelasticity". International Journal of Fracture. 166 (1–2): 91–103. doi:10.1007/s10704-010-9502-9. ISSN 0376-9429.
- ^ Jobin, T.M.; Ramji, M.; Khaderi, S.N. (2019). "Numerical evaluation of the interaction of rigid line inclusions using strain intensity factors". International Journal of Mechanical Sciences. 153–154: 10–20. doi:10.1016/j.ijmecsci.2019.01.017.
- ^ Bigoni, D. Nonlinear Solid Mechanics: Bifurcation Theory and Material Instability. Cambridge University Press, 2012 . ISBN 9781107025417.
- ^ Dal Corso, Francesco; Bigoni, Davide; Gei, Massimiliano (2008). "The stress concentration near a rigid line inclusion in a prestressed, elastic material. Part I.Full-field solution and asymptotics". Journal of the Mechanics and Physics of Solids. 56 (3): 815–838. Bibcode:2008JMPSo..56..815D. doi:10.1016/j.jmps.2007.07.002. ISSN 0022-5096.
- ^ Bigoni, Davide; Dal Corso, Francesco; Gei, Massimiliano (2008). "The stress concentration near a rigid line inclusion in a prestressed, elastic material. Part II.Implications on shear band nucleation, growth and energy release rate". Journal of the Mechanics and Physics of Solids. 56 (3): 839–857. Bibcode:2008JMPSo..56..839B. doi:10.1016/j.jmps.2007.07.003. ISSN 0022-5096.
- ^ Dal Corso, Francesco; Bigoni, Davide (2008). "The interactions between shear bands and rigid lamellar inclusions in a ductile metal matrix". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 465 (2101): 143–163. doi:10.1098/rspa.2008.0242. ISSN 1364-5021.
